有限自动机与序列识别
子字符串搜索是指给定一段文本,需要在其中找到想要的字符串;如果将文本换成输入流,那么问题就转换成了序列识别;而有限自动机则是一个能够在线性时间内完成以上任务的一种数学模型。
1 使用有限自动机进行子字符串搜索的基本过程
AUGGCUCCUCUGUAA
假设这是mRNA上的一串密码子,而我们想要找到这串序列中密码子CCU的位置。
1.1 定义状态
要使用有限自动机来完成这个任务,首先需要设置读取过程中的状态,为此,我们做出以下定义:
状态0: 未读取到任何符合的字符
状态1: 读取到一个符合的字符,在上面的例子中即读取到碱基C
状态2: 连续读取到两个符合的字符,即连续读取到两个碱基C
状态3: 读取到所有符合的字符,匹配成功,即检测到密码子CCU
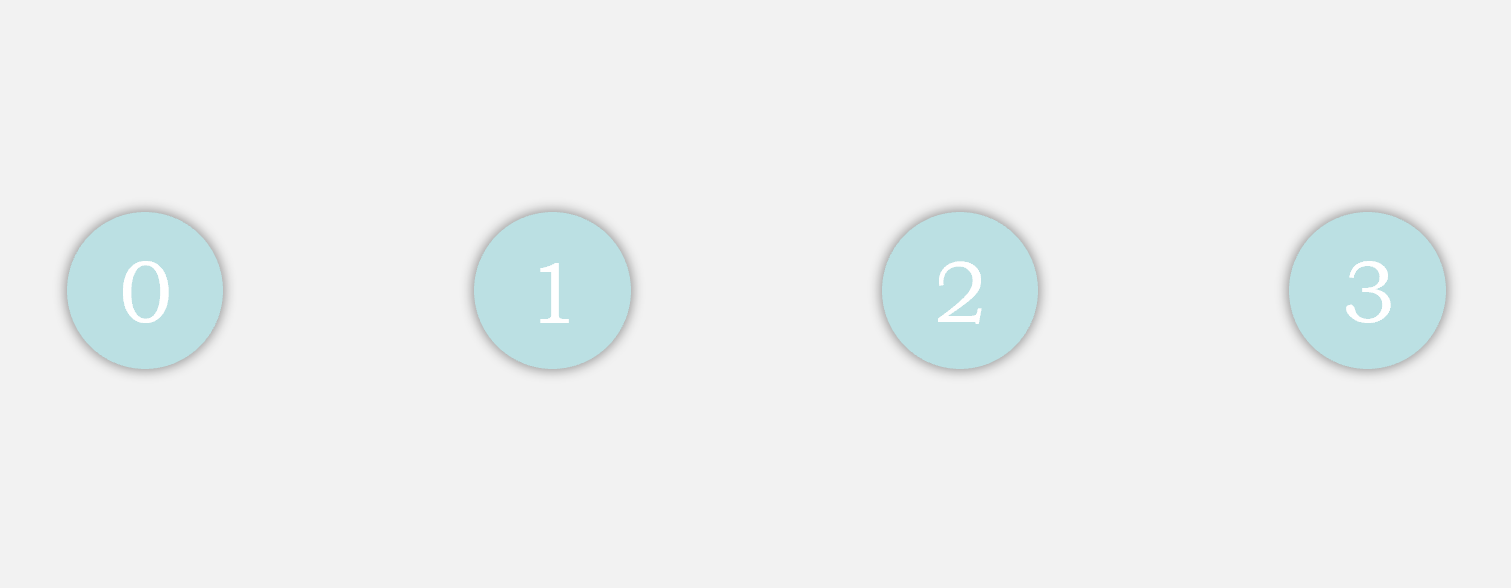
1.2 确定状态转移
有限自动机的初始状态为0,我们一个一个地从文本中读取字符,根据读取到的字符,我们要确定有限自动机会到达的下一个状态,当达到状态3时,我们的目标才算是完成了。
举个例子,如果我们第一个读取的字符是A,这并不是我们所需要检测的第一个字符,则状态机仍然会处于状态0;但是如果我们读取的字符是C,这正是目标密码子的第一个字符,根据定义,自动机到达状态1。
如果下一个字符幸运的还是C,我们则可以继续前进到达状态2;如果不幸地检测到了G,则目前检测到的是CG,和我们的目标没法重叠,我们只能无奈地回到状态0。
当我们处在状态2时,再读取到一个U即可大功告成,但若是读取到的还是C(不考虑这种情况在生命科学中是否存在),我们既不用退回到状态0也不会退回到状态1,我们仍然会处于状态2,因为我们当前检测到的序列是CCC,如果取后两个C,我们还是符合状态2的定义,现在只需把第一个C丢掉不管即可。所以有限自动机的检测是允许重叠的,读取到一个不符合期望的字符时不一定会退回状态0,除非我们要求必须一次性读取到全部目标字符。
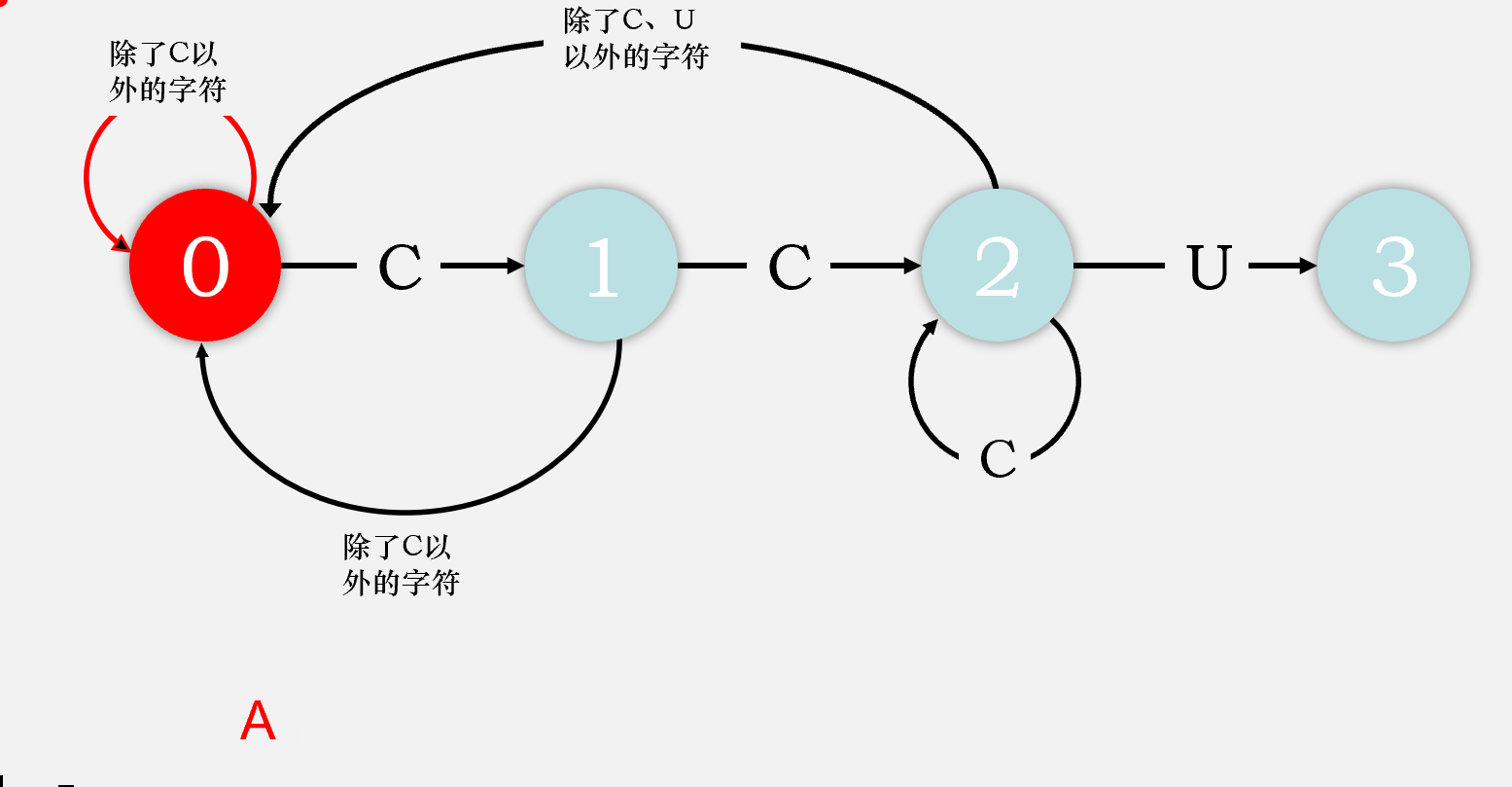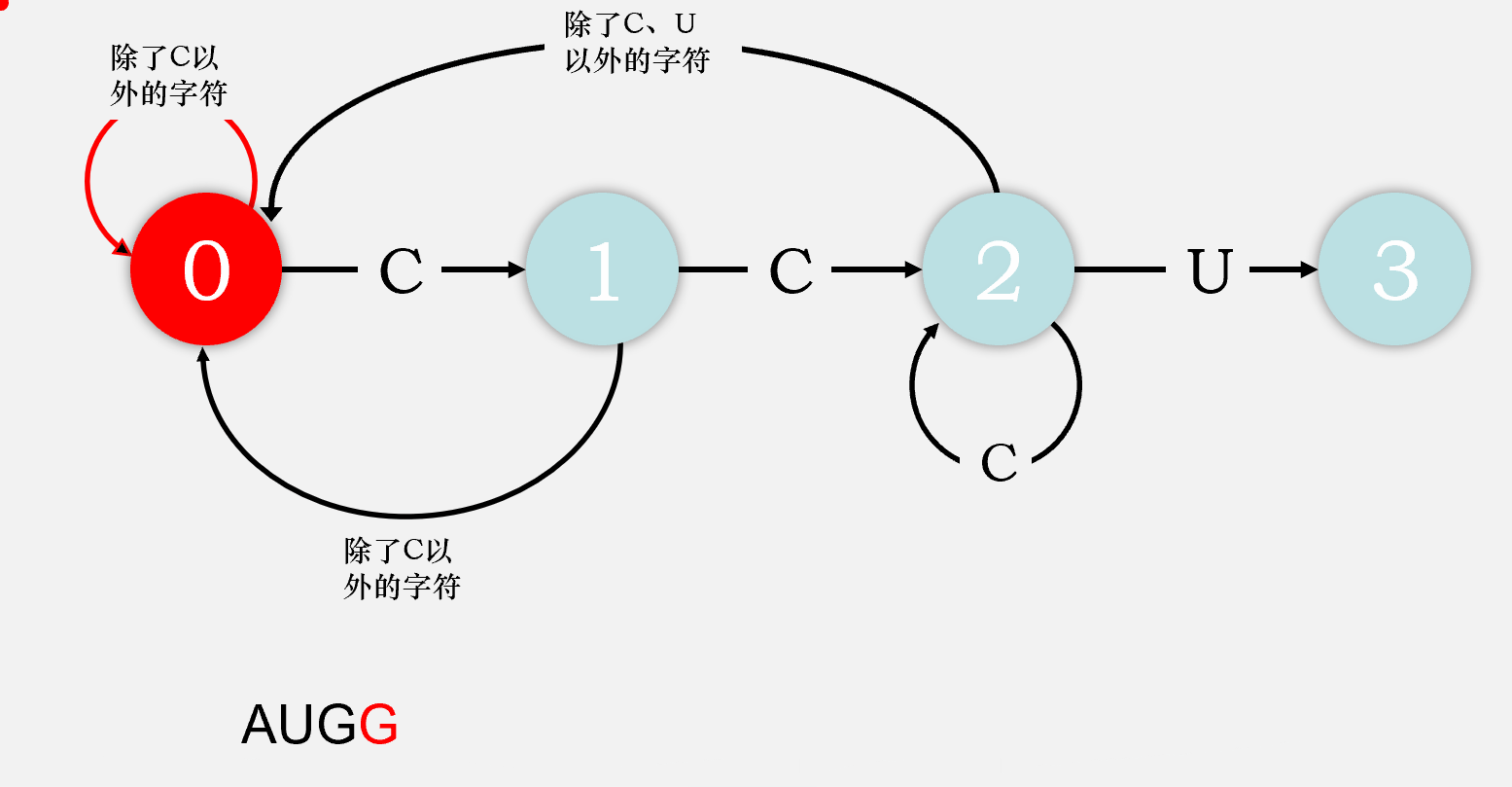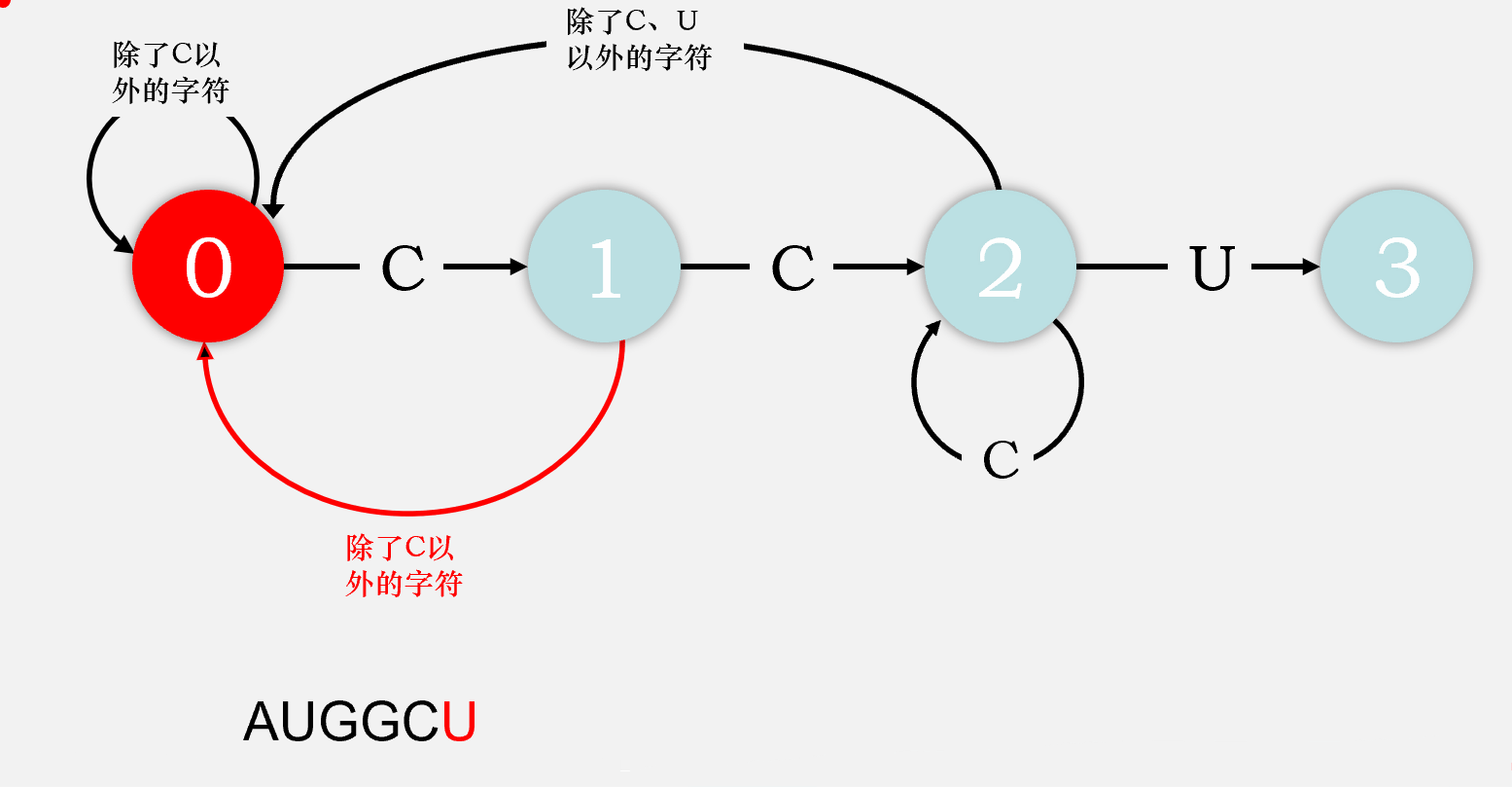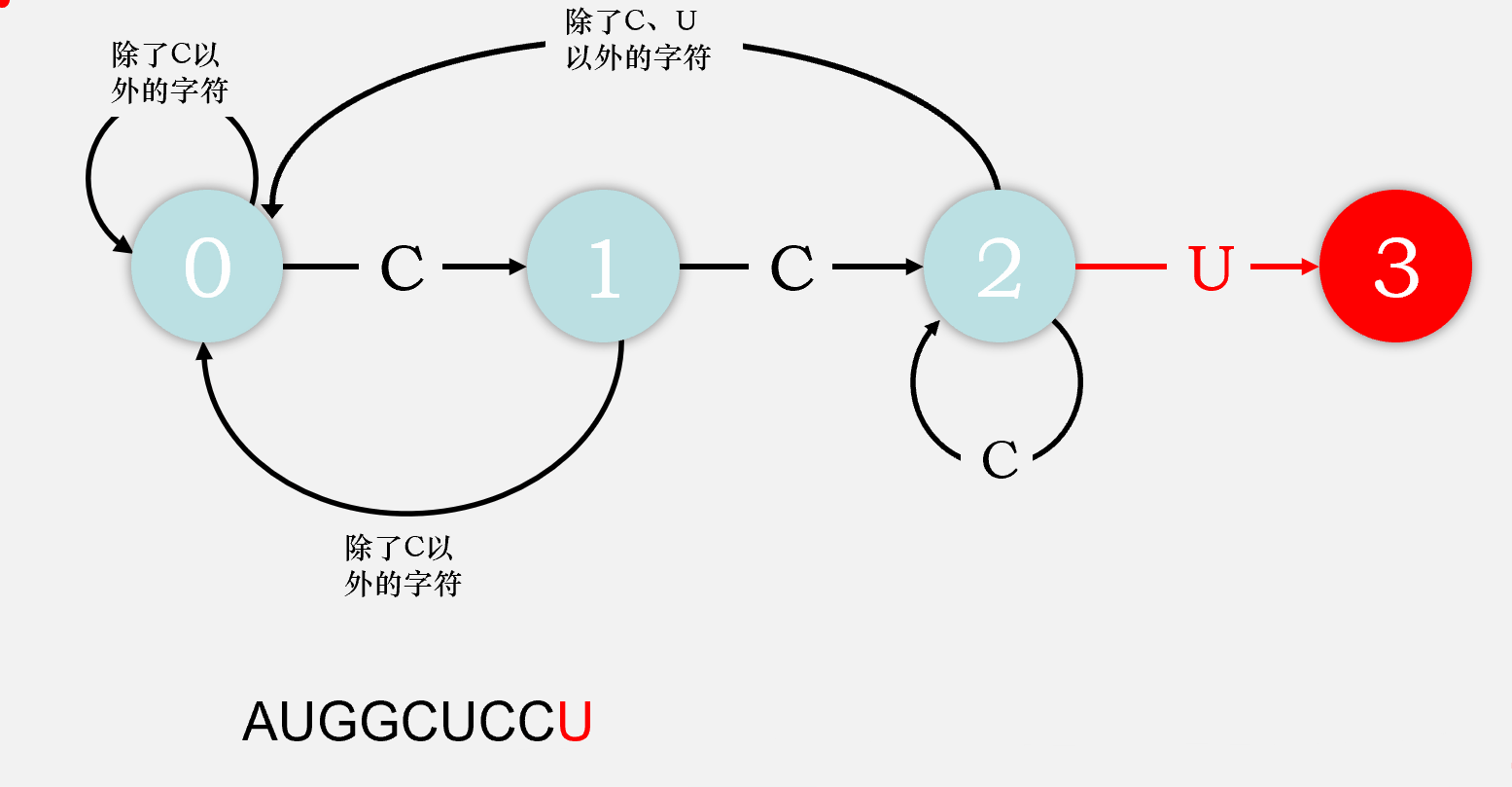
由此,我们可以画出完整的状态转移图,同时得到状态转移图的矩阵表示:

| 0 | 1 | 2 | |
|---|---|---|---|
| C | 1 | 2 | 2 |
| U | 0 | 0 | 3 |
| A | 0 | 0 | 0 |
| ... | 0 | 0 | 0 |
| Z | 0 | 0 | 0 |
按照以上步骤,给定非空有穷的状态集合、非空有穷的输入字母表、状态转移函数、初始状态、终止状态,则最终得到了有限自动机。而上面这个自动机,对于每个状态和每个输入字符,可以完全确定唯一的后继状态,则称为确定型有穷自动机(deterministic finite automata, DFA)。
我们定义一个二维数组int[R][j] dfa来表示上面的状态转移矩阵,R是输入字母表的字母个数,j是当前所处的状态,dfa[c][j]代表状态j下读取到字符c后的后继状态,该矩阵描述了状态转移函数。
对于我们要处理的问题,矩阵dfa是一个稀疏(sparse)矩阵,大部分元素是0,如果输入字母表是ASCII码表(128个字符)或者Unicode(65536个),则情况更甚。
1.3 根据状态转移表完成我们的任务
初始化自动机,状态j = 0,
读取第一个字符,为A,
dfa['A'][0] = 0,仍在状态0读取第二个字符,为U,
dfa['U'][0] = 0,仍在状态0......
读取第五个字符,为C,
dfa['C'][0] = 1,到达状态1读取第六个字符,为U,
dfa['U'][1] = 0,回到状态0读取第七个字符,为C,
dfa['C'][0] = 1,到达状态1读取第八个字符,为C,
dfa['C'][1] = 2,到达状态2读取第九个字符,为U,
dfa['U'][2] = 3,到达状态3,算法终止
2 如何用代码自动生成DFA?
给定一个要检测的序列,最容易构建的显然是DFA的主干部分,即从状态0到状态1,从状态1到状态2...从状态n-1到状态n的路径
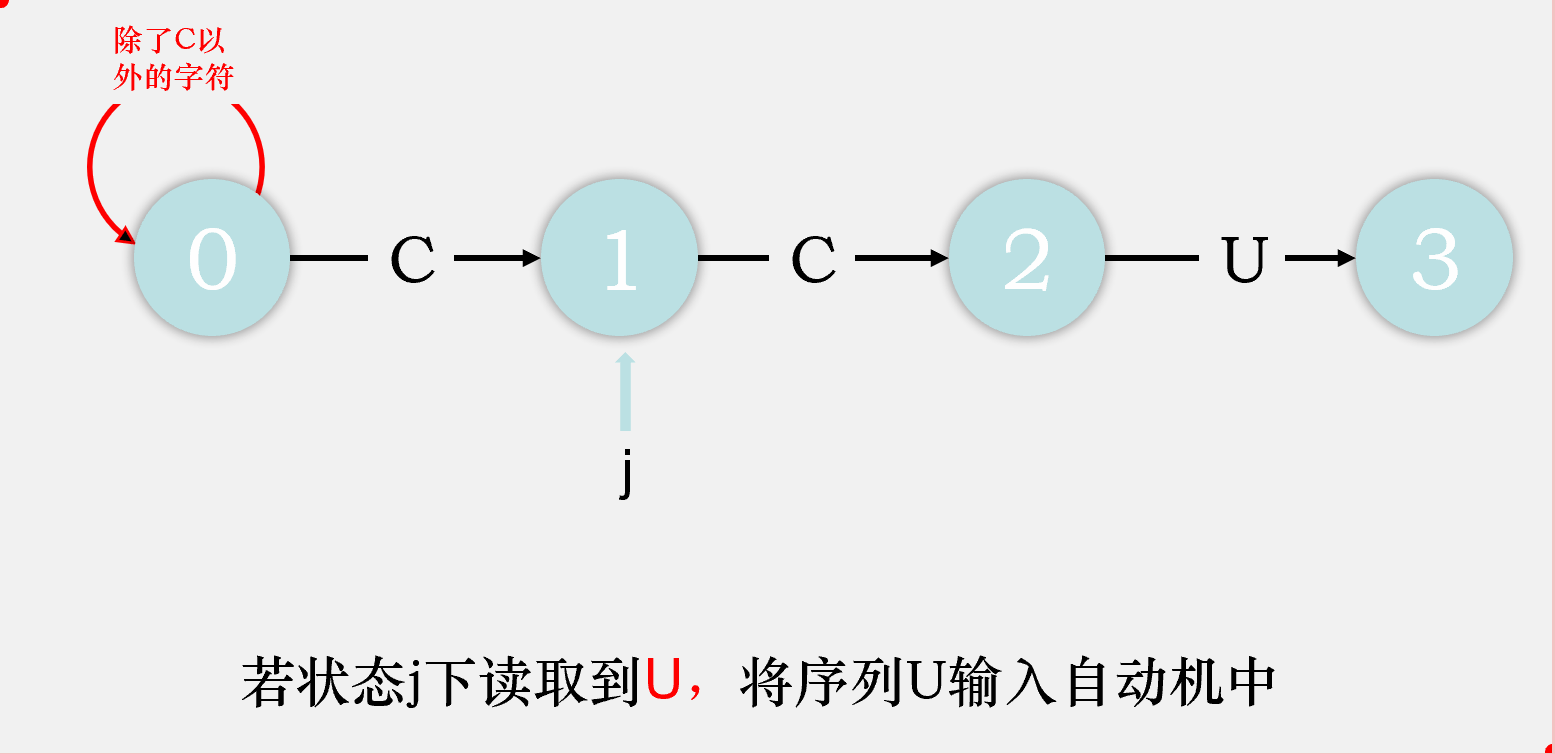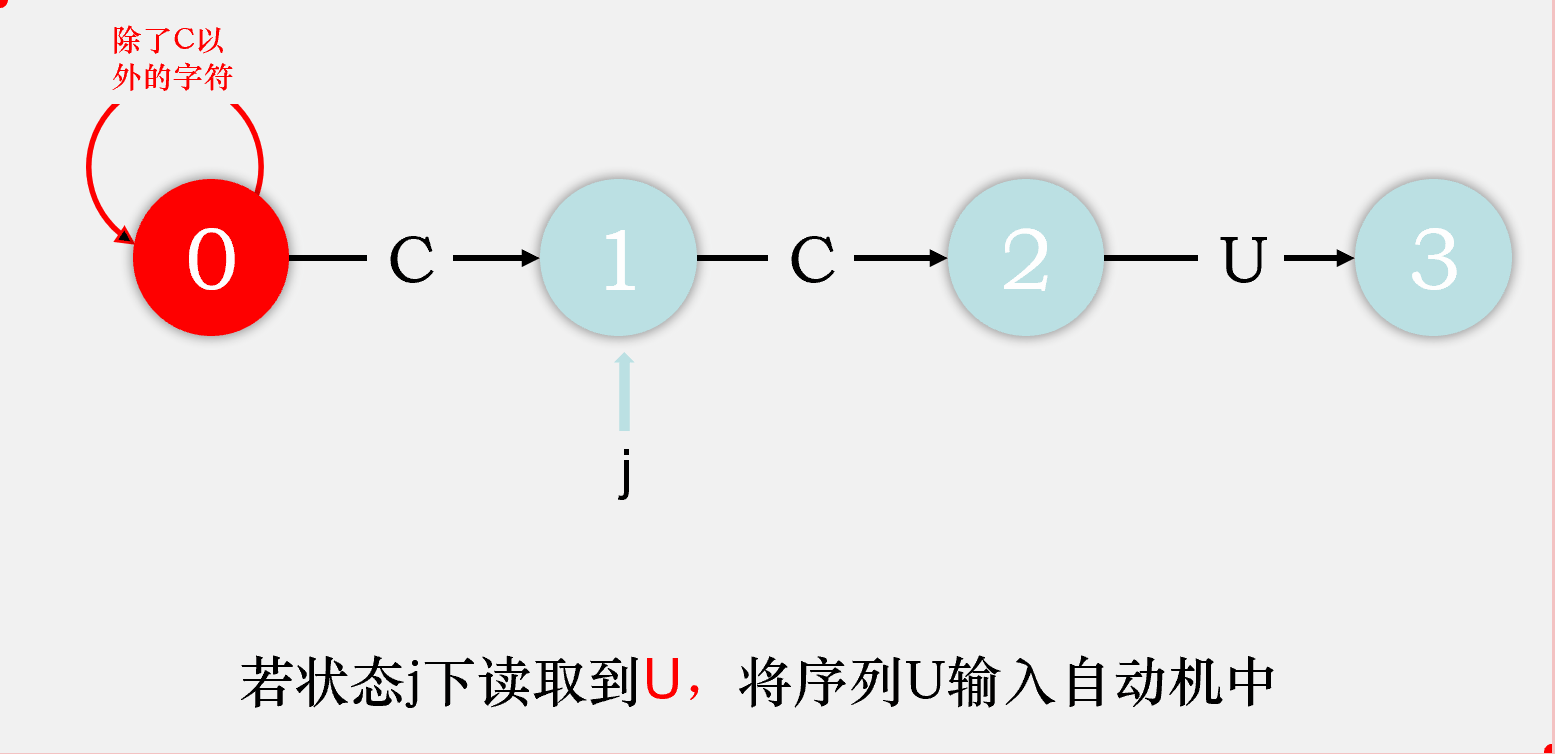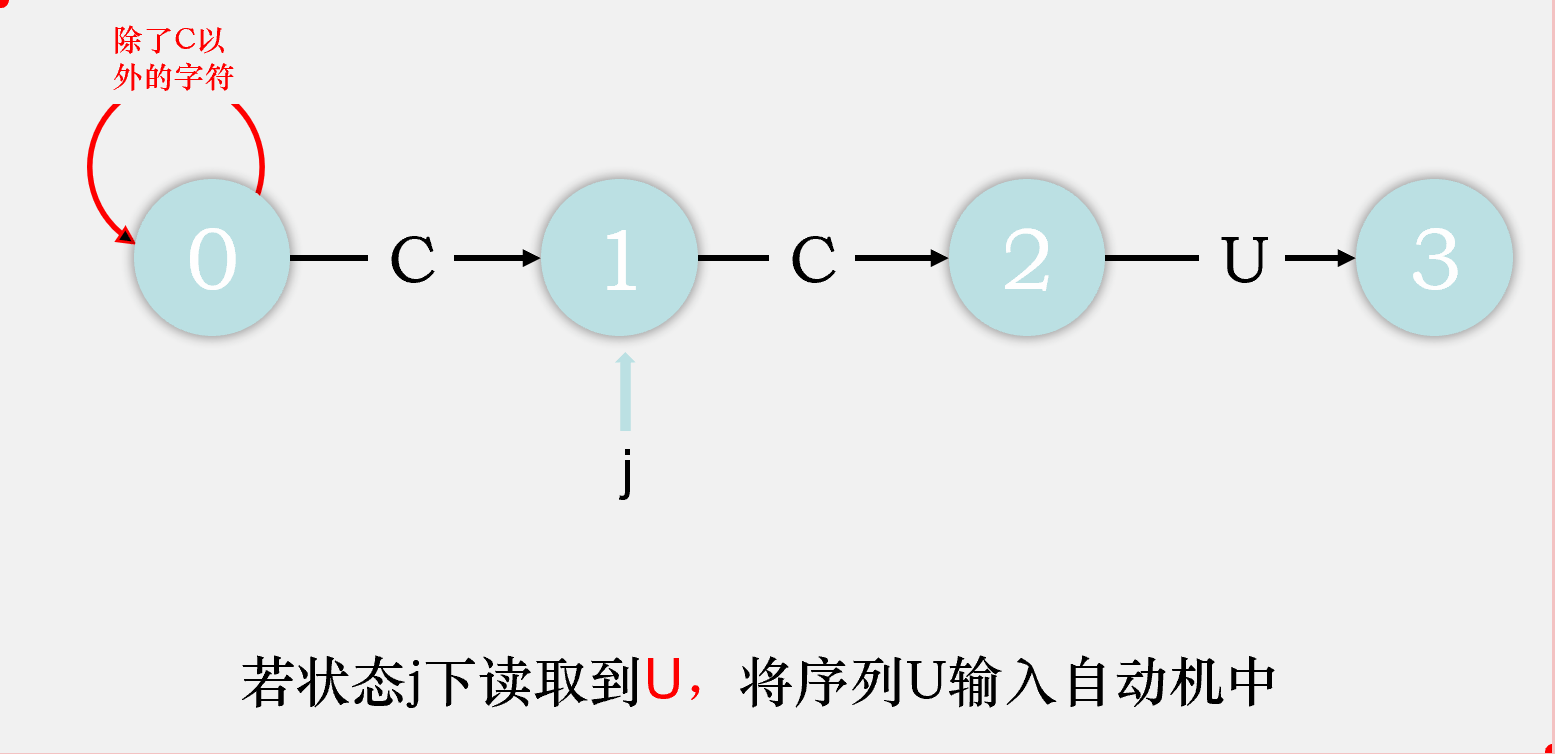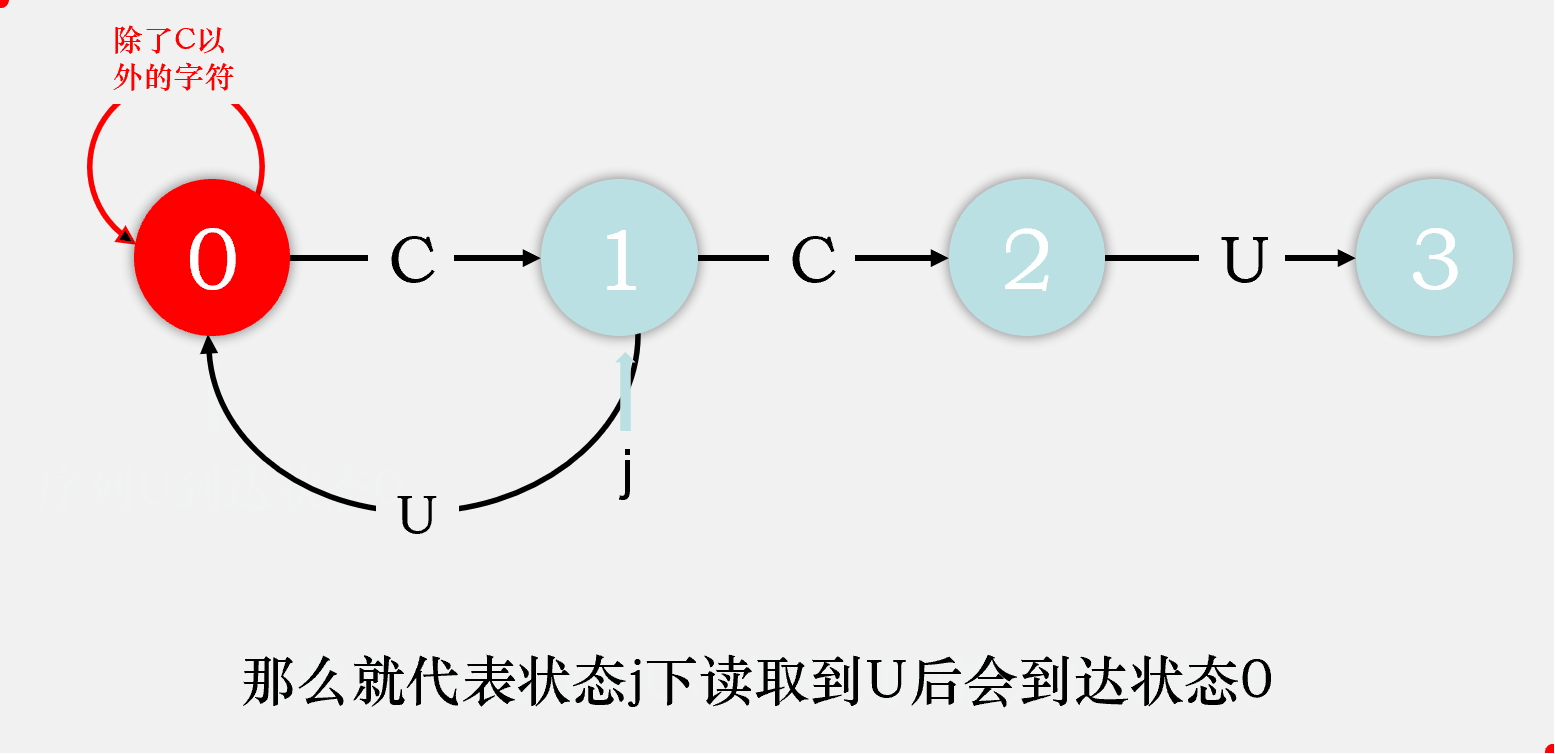
对于剩下的匹配失败时的状态转移,我们可以这样考虑,由于在状态j读到了一个不满足期望的字符char,则目前读到的整个序列[0...j]都是不满足要求的,那么我们则剔除序列中的第一个字符,检验序列[1...j]输入自动机后会到达什么状态,该状态就是状态j读取char时会到达的状态。我们先将序列[1...j-1]输入状态机,检验其会达到什么状态,将这个状态称为重启状态x,再在这个状态下输入字符char,检验会到达什么状态,该状态即为状态j匹配char时会到达的状态。
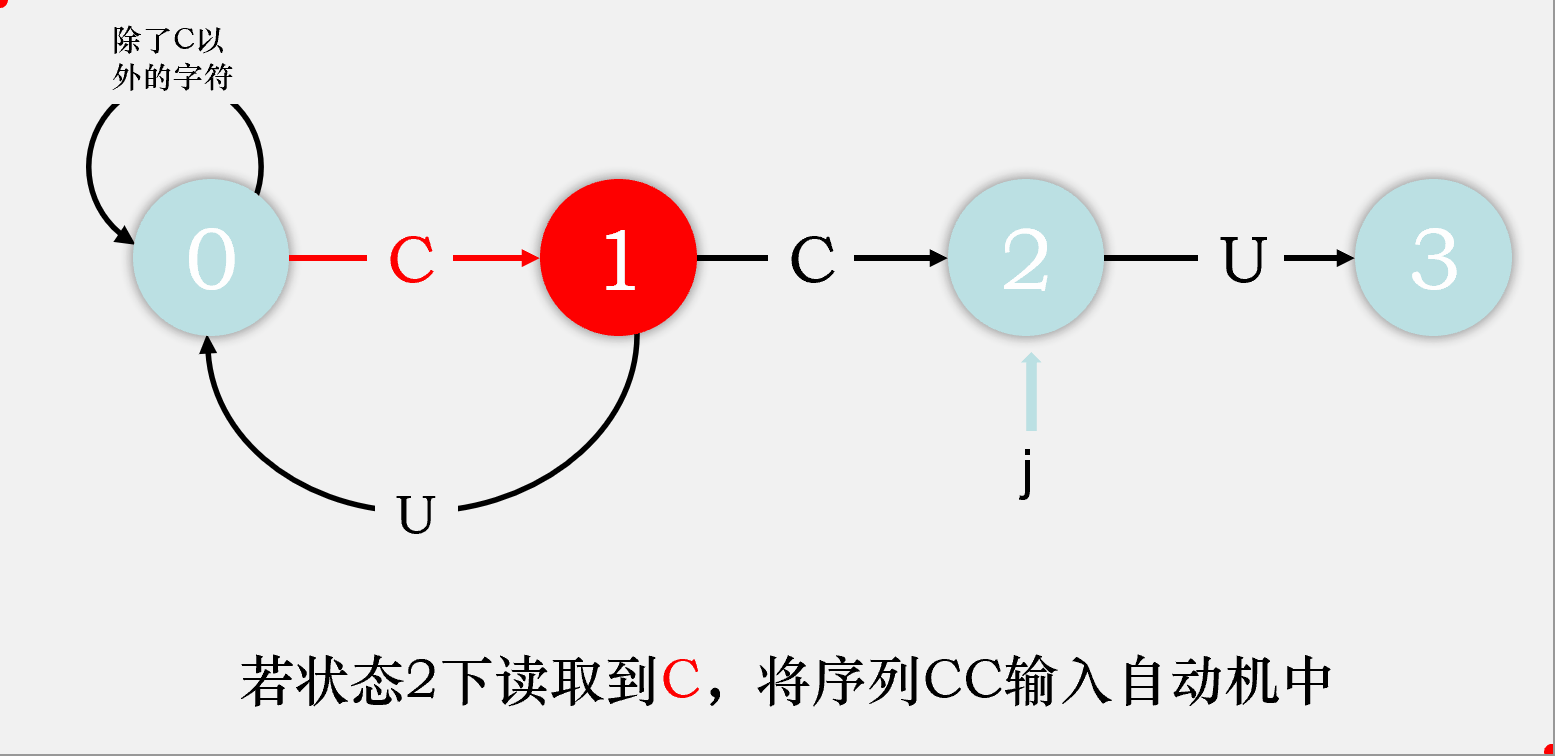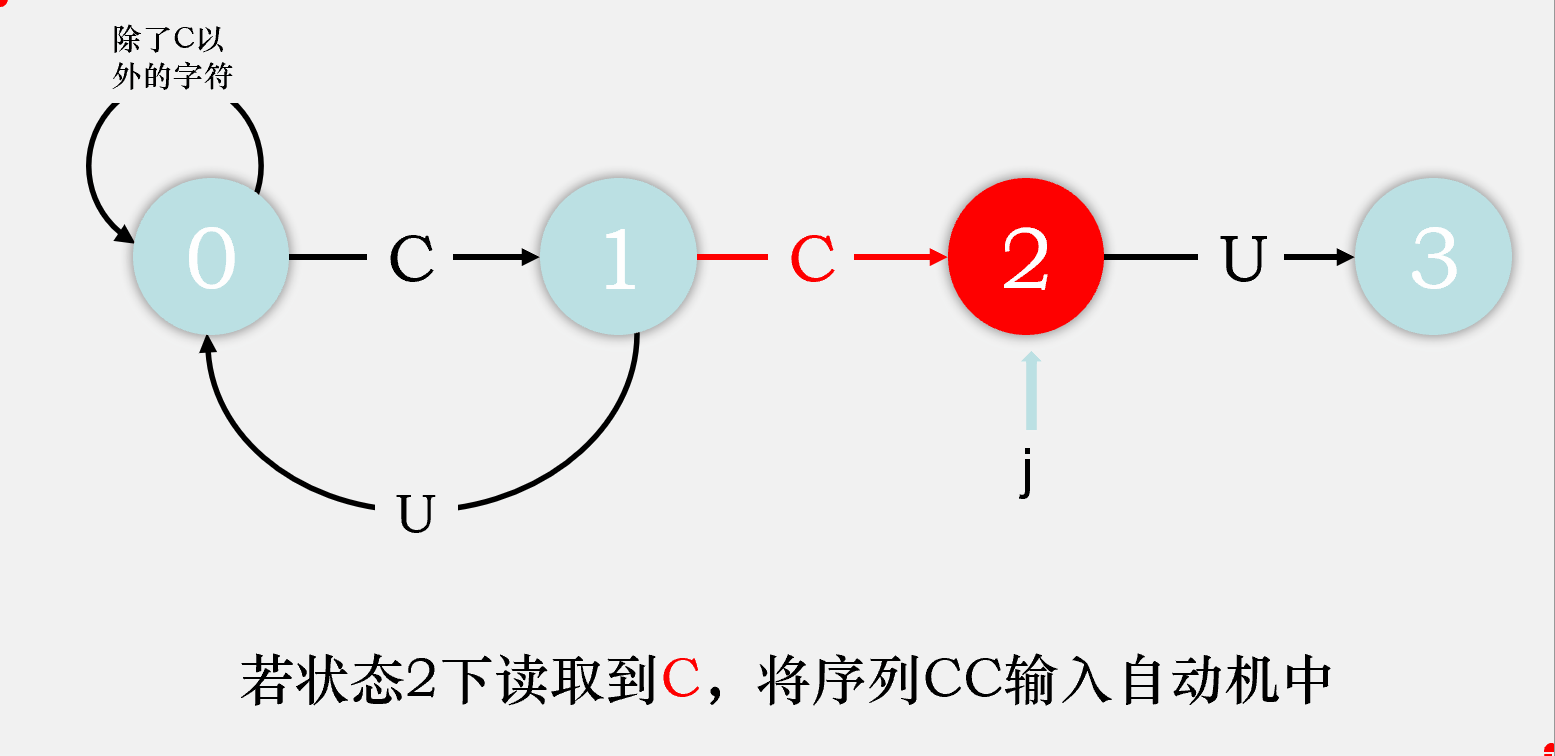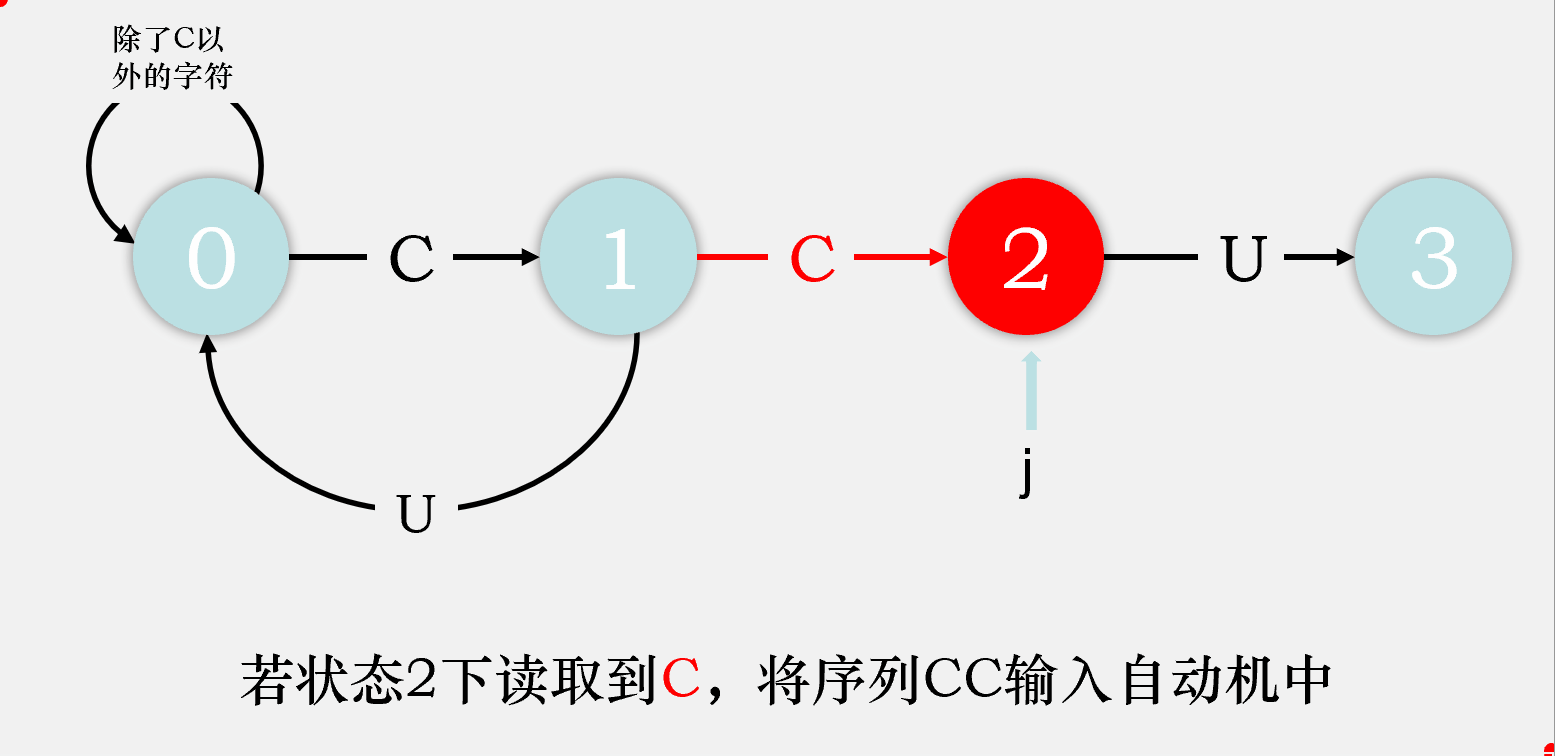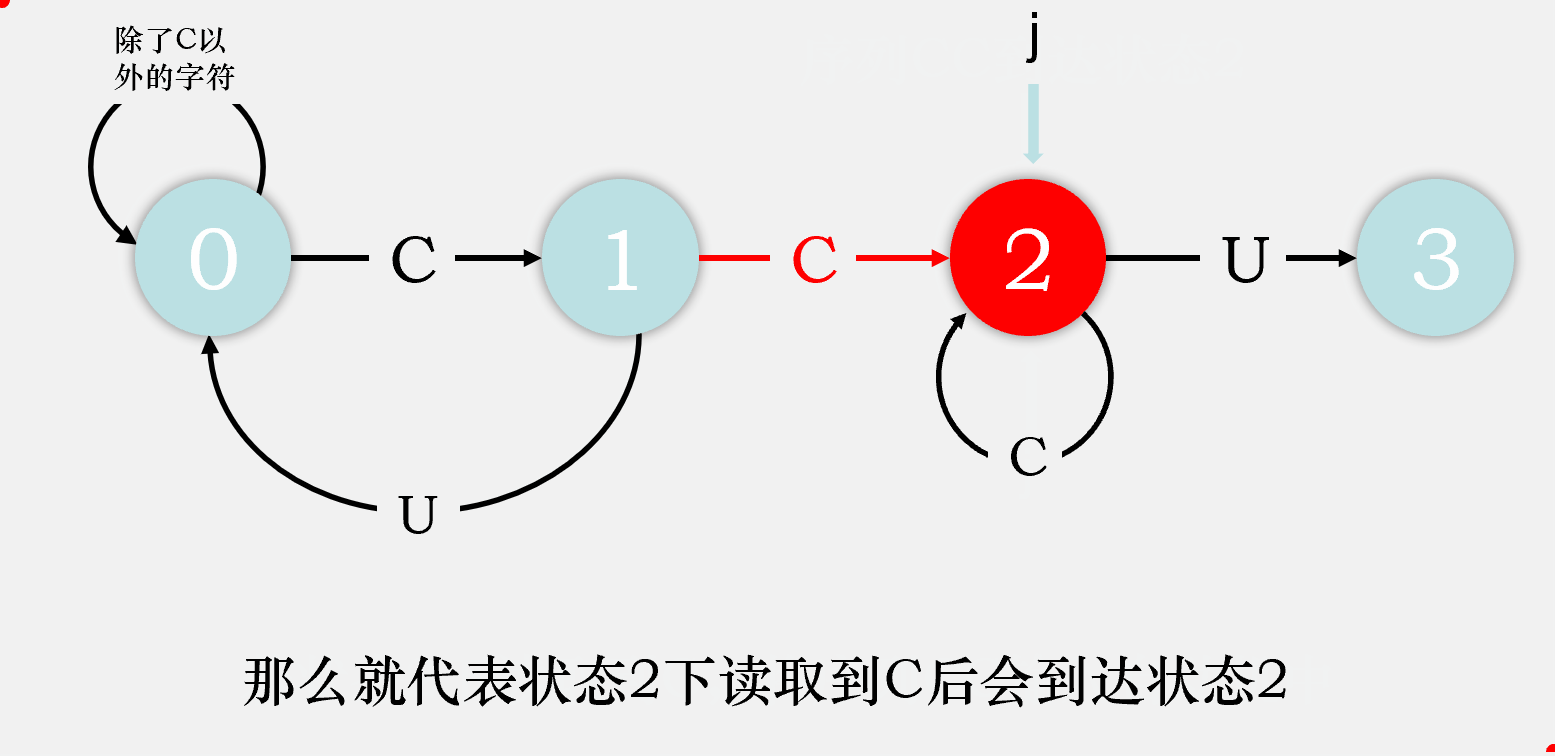
比如说,我们在状态2下匹配到了C,则目前读取到的序列是CCC,我们去掉第一个字符,将第二个字符C输入状态机,最终达到状态1,则状态2重启状态为状态1,再将匹配失败的那个字符C输入状态1,最终到达状态2,则dfa['C'][2] = dfa['C'][1] = 2,即目前我们匹配成功的字符数目还是2个。
故我们可以得出dfa[匹配失败字符][j] = dfa[匹配失败字符][x], dfa[匹配成功字符][j] = j + 1。
上述过程的代码如下:
1 | public void DFAConstruct(String pat) |